Complex number

From Wikipedia, the free encyclopedia

A complex number can be visually represented as a pair of numbers forming a vector on a diagram called an Argand diagram

In mathematics, the complex numbers are an extension of the real numbers obtained by adjoining an imaginary unit, denoted i, which satisfies:^[1]

$i^2=-1.\,$

Every complex number can be written in the form a + bi, where a and b are real numbers called the real part and the imaginary part of the complex number, respectively.

Complex numbers are a field, and thus have addition, subtraction, multiplication, and division operations. These operations extend the corresponding operations on real numbers, although with a number of additional elegant and useful properties, e.g., negative real numbers can be obtained by squaring complex (imaginary) numbers.

Complex numbers were first discovered by the Italian mathematician Girolamo Cardano, who called them "fictitious", during his attempts to find solutions to cubic equations.^[2] The solution of a general cubic equation may require intermediate calculations containing the square roots of negative numbers, even when the final solutions are real numbers, a situation known as casus irreducibilis. This ultimately led to the fundamental theorem of algebra, which shows that with complex numbers, it is always possible to find solutions to polynomial equations of degree one or higher.

Definitions

[edit] Notation

The set of all complex numbers is usually denoted by C, or in blackboard bold by $\mathbb{C}$ .

Although other notations can be used, complex numbers are very often written in the form

$a + bi \,$

where a and b are real numbers, and i is the imaginary unit, which has the property i² = −1. The real number a is called the real part of the complex number, and the real number b is the imaginary part.

For example, 3 + 2i is a complex number, with real part 3 and imaginary part 2. If z = a + ib, the real part a is denoted Re(z) or ℜ(z), and the imaginary part b is denoted Im(z) or ℑ(z).

The real numbers, R, may be regarded as a subset of C by considering every real number a complex number with an imaginary part of zero; that is, the real number a is identified with the complex number a + 0i. Complex numbers with a real part of zero are called imaginary numbers; instead of writing 0 + bi, that imaginary number is usually denoted as just bi. If b equals 1, instead of using 0 + 1i or 1i, the number is denoted as i.

In some disciplines (in particular, electrical engineering, where i is a symbol for current), the imaginary unit i is instead written as j, so complex numbers are sometimes written as a + bj.

Domain coloring plot of the function
ƒ(x) =(x² − 1)(x − 2 − i)²/(x² + 2 + 2i). The hue represents the function argument, while the saturation represents the magnitude.

[edit] Equality

Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. In other words, if the two complex numbers are written as a + bi and c + di with a, b, c, and d real, then they are equal if and only if a = c and b = d.

[edit] Operations

Complex numbers are added, subtracted, multiplied, and divided by formally applying the associative, commutative and distributive laws of algebra, together with the equation i² = −1:

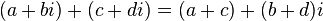
Addition: $\,(a + bi) + (c + di) = (a + c) + (b + d)i$
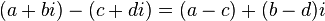
Subtraction: $\,(a + bi) - (c + di) = (a - c) + (b - d)i$
Multiplication: $\,(a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i$
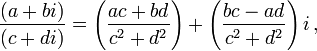
Division: $\,\frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\,,$

where c and d are not both zero.

It is also possible to represent complex numbers as ordered pairs of real numbers, so that the complex number a + ib corresponds to (a, b). In this representation, the algebraic operations have the following formulas:

(a, b) + (c, d) = (a + c, b + d)

(a, b)(c, d) = (ac − bd, bc + ad)

Since the complex number a + bi is uniquely specified by the ordered pair (a, b), the complex numbers are in one-to-one correspondence with points on a plane. This complex plane is described below.

he complex plane

Geometric representation of

z

and its conjugate $\bar{z}$ in the complex plane.

A complex number z can be viewed as a point or a position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand diagram (see Pedoe 1988 and Solomentsev 2001) named after Jean-Robert Argand. The point and hence the complex number z can be specified by Cartesian (rectangular) coordinates. The Cartesian coordinates of the complex number are the real part x = Re(z) and the imaginary part y = Im(z). The representation of a complex number by its Cartesian coordinates is called the Cartesian form or rectangular form or algebraic form of that complex number.

[edit] Absolute value, conjugation and distance

The absolute value (or modulus or magnitude) of a complex number $z = r e i φ$ is defined as $| z | = r$ . Algebraically, if $z = x + y i$ , then $|z|=\sqrt{x^2+y^2}.$

The absolute value has three important properties:

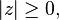$| z | \geq 0, \,$ where $| z | = 0 \,$ if and only if $z = 0 \,$

$| z + w | \leq | z | + | w | \,$ (triangle inequality)

$| z \cdot w | = | z | \cdot | w | \,$

for all complex numbers z and w. These imply that $| 1 | = 1$ and $| z / w | = | z | / | w |$ . By defining the distance function $d (z, w) = | z - w |$ , we turn the set of complex numbers into a metric space and we can therefore talk about limits and continuity.

The complex conjugate of the complex number $z = x + y i$ is defined to be $x - y i$ , written as $\bar{z}$ or $z^*\,$ . As seen in the figure, $\bar{z}$ is the "reflection" of z about the real axis, and so both $z+\bar{z}$ and $z\cdot\bar{z}$ are real numbers. Many identities relate complex numbers and their conjugates:

$\overline{z+w} = \bar{z} + \bar{w}$

$\overline{z\cdot w} = \bar{z}\cdot\bar{w}$

$\overline{(z/w)} = \bar{z}/\bar{w}$

$\bar{\bar{z}}=z$

$\bar{z}=z$ if and only if z is real

$\bar{z}=-z$ if and only if z is purely imaginary

$\operatorname{Re}\,(z) = \tfrac{1}{2}(z+\bar{z})$

$\operatorname{Im}\,(z) = \tfrac{1}{2i}(z-\bar{z})$

$|z|=|\bar{z}|$

$|z|^2 = z\cdot\bar{z}$

$z^{-1} = \frac{\bar{z}}{|z|^{2}}$ if z is non-zero.

Matrix representation of complex numbers

While usually not useful, alternative representations of the complex field can give some insight into its nature. One particularly elegant representation interprets each complex number as a 2×2 matrix with real entries which stretches and rotates the points of the plane. Every such matrix has the form

$\begin{bmatrix} a & -b \\ b & \;\; a \end{bmatrix}$

where a and b are real numbers. The sum and product of two such matrices is again of this form, and the product operation on matrices of this form is commutative. Every non-zero matrix of this form is invertible, and its inverse is again of this form. Therefore, the matrices of this form are a field, isomorphic to the field of complex numbers. Every such matrix can be written as

$\begin{bmatrix} a & -b \\ b & \;\; a \end{bmatrix} = a \begin{bmatrix} 1 & \;\; 0 \\ 0 & \;\; 1 \end{bmatrix} + b \begin{bmatrix} 0 & -1 \\ 1 & \;\; 0 \end{bmatrix}$

which suggests that we should identify the real number 1 with the identity matrix

$\begin{bmatrix} 1 & \;\; 0 \\ 0 & \;\; 1 \end{bmatrix},$

and the imaginary unit i with

$\begin{bmatrix} 0 & -1 \\ 1 & \;\; 0 \end{bmatrix},$

a counter-clockwise rotation by 90 degrees. Note that the square of this latter matrix is indeed equal to the 2×2 matrix that represents −1.

The square of the absolute value of a complex number expressed as a matrix is equal to the determinant of that matrix.

$|z|^2 = \begin{vmatrix} a & -b \\ b & a \end{vmatrix} = (a^2) - ((-b)(b)) = a^2 + b^2.$

If the matrix is viewed as a transformation of the plane, then the transformation rotates points through an angle equal to the argument of the complex number and scales by a factor equal to the complex number's absolute value. The conjugate of the complex number z corresponds to the transformation which rotates through the same angle as z but in the opposite direction, and scales in the same manner as z; this can be represented by the transpose of the matrix corresponding to z.

If the matrix elements are themselves complex numbers, the resulting algebra is that of the quaternions. In other words, this matrix representation is one way of expressing the Cayley-Dickson construction of algebras.

It should also be noted that the two eigenvalues of the 2x2 matrix representing a complex number are the complex number itself and its conjugate.

[edit] Real vector space

C is a two-dimensional real vector space. Unlike the reals, the set of complex numbers cannot be totally ordered in any way that is compatible with its arithmetic operations: C cannot be turned into an ordered field. More generally, no field containing a square root of −1 can be ordered.

R-linear maps C → C have the general form

$f(z)=az+b\overline{z}$

with complex coefficients a and b. Only the first term is C-linear, and only the first term is holomorphic; the second term is real-differentiable, but does not satisfy the Cauchy-Riemann equations.

The function

$f(z)=az\,$

corresponds to rotations combined with scaling, while the function

$f(z)=b\overline{z}$

corresponds to reflections combined with scaling

~ L A L A L A Z O N E ~

Friday, October 24, 2008

Complex number

From Wikipedia, the free encyclopedia

Definitions

[edit] Notation

[edit] Equality

[edit] Operations

he complex plane

[edit] Absolute value, conjugation and distance

Matrix representation of complex numbers

[edit] Real vector space

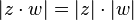
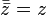
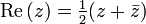
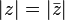
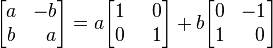
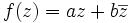
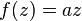
No comments:

Anak sapa la nie...?

Teman mike...

Gile Manga.

Skod2..(0.o)