Friday, October 24, 2008

Trigonometry

From Wikipedia, the free encyclopedia

The Canadarm2 robotic manipulator on the International Space Station is operated by controlling the angles of its joints. Calculating the final position of the astronaut at the end of the arm requires repeated use of the trigonometric functions of those angles.
The Canadarm2 robotic manipulator on the International Space Station is operated by controlling the angles of its joints. Calculating the final position of the astronaut at the end of the arm requires repeated use of the trigonometric functions of those angles.
All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O.
All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O.

Trigonometry (from Greek trigōnon "triangle" + metron "measure")[1] is a branch of mathematics that deals with triangles, particularly those plane triangles in which one angle has 90 degrees (right triangles). Trigonometry deals with relationships between the sides and the angles of triangles and with the trigonometric functions, which describe those relationships.

Trigonometry has applications in both pure mathematics and in applied mathematics, where it is essential in many branches of science and technology. It is usually taught in secondary schools either as a separate course or as part of a precalculus course. Trigonometry is informally called "trig".

Overview

In this right triangle: sin A = a/c; cos A = b/c; tan A = a/b.
In this right triangle: sin A = a/c; cos A = b/c; tan A = a/b.

If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a right triangle is completely determined, up to similarity, by the angles. This means that once one of the other angles is known, the ratios of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:

  • The sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
\sin A=\frac{\textrm{opposite}}{\textrm{hypotenuse}}=\frac{a}{\,c\,}\,.
  • The cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.
\cos A=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{b}{\,c\,}\,.
  • The tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.
\tan A=\frac{\textrm{opposite}}{\textrm{adjacent}}=\frac{a}{\,b\,}=\frac{\sin A}{\cos A}\,.

Common formulae

Main article: Trigonometric identity
Main article: Trigonometric function

Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. Many express important geometric relationships. For example, the Pythagorean identities are an expression of the Pythagorean Theorem. Here are some of the more commonly used identities, as well as the most important formulae connecting angles and sides of an arbitrary triangle. For more identities see trigonometric identity.

[edit] Trigonometric identities


[edit] Pythagorean identities

\begin{align} \sin^2 \alpha + \cos^2 \alpha = 1 \\ \tan^2 \alpha + 1 = \sec^2 \alpha \\ 1+\cot^2 \alpha = \csc^2 \alpha \end{align}

[edit] Sum and product identities

[edit] Sum to product
\begin{align} \sin \alpha \pm \sin \beta &= 2\sin \left( \frac{\alpha \pm \beta}{2}\right)\cos \left(\frac{\alpha \mp \beta}{2} \right)\\ \cos \alpha + \cos \beta &= 2\cos \left(\frac{\alpha + \beta}{2} \right)\cos \left(\frac{\alpha - \beta}{2}\right)\\ \cos \alpha - \cos \beta &= -2\sin \left(\frac{\alpha + \beta}{2} \right) \sin \left(\frac{\alpha - \beta}{2}\right)\\ &= 2\sin \left(\frac{\alpha + \beta}{2} \right) \sin \left(\frac{\beta - \alpha}{2}\right) \end{align}

[edit] Product to sum[3]
\begin{align} \cos \alpha \,\cos \beta &= \frac{1}{2}[\cos(\alpha - \beta) + \cos (\alpha + \beta)]\\ \sin \alpha \,\sin \beta &= \frac{1}{2}[\cos(\alpha - \beta) - \cos (\alpha + \beta)]\\ \cos \alpha \,\sin \beta &= \frac{1}{2}[\sin(\alpha + \beta) - \sin (\alpha - \beta)]\\ \sin \alpha \,\cos \beta &= \frac{1}{2}[\sin(\alpha + \beta) + \sin (\alpha - \beta)] \end{align}

[edit] Sine, cosine, and tangent of a sum

Detailed, diagramed proofs of the first two of these formulas are available
for download as a four-page PDF document at Image:Sine Cos Proofs.pdf.

\begin{align} \sin(\alpha \pm \beta) &= \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos(\alpha \pm \beta) &= \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ \tan(\alpha \pm \beta) &= \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \end{align}

[edit] Half-angle identities

Note that \pm is correct, it means it may be either one, depending on the value of A/2.

\begin{align} \sin \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{2}} \\ \cos \frac{A}{2} &= \pm \sqrt{\frac{1+\cos A}{2}} \\\tan \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \end{align}

[edit] Stereographic (or parametric) identities

\begin{align} \sin \alpha &= \frac{2T}{1+T^2} \\ \cos \alpha &= \frac{1-T^2}{1+T^2}\\ \end{align}

where T=\tan \frac{\alpha}{2}.

[edit] Triangle identities

Laws of Sines and Cosines
Laws of Sines and Cosines\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} \cos C=\frac{a^2+b^2-c^2}{2ab}

In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.

[edit] Law of sines

The law of sines (also know as the "sine rule") for an arbitrary triangle states:

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,

where R is the radius of the circumcircle of the triangle.

[edit] Law of cosines

The law of cosines (also known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:

c^2=a^2+b^2-2ab\cos C ,\,

or equivalently:

\cos C=\frac{a^2+b^2-c^2}{2ab}.\,

[edit] Law of tangents

The law of tangents:

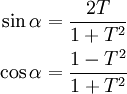
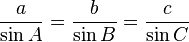
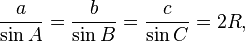
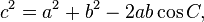
\frac{a+b}{a-b}=\frac{\tan\left[\tfrac{1}{2}(A+B)\right]}{\tan\left[\tfrac{1}{2}(A-B)\right]}
Flying without wings by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)