Polynomial
From Wikipedia, the free encyclopedia
Overview
A polynomial is either zero, or can be written as the sum of one or more non-zero terms. The number of terms is finite. These terms consist of a constant (called the coefficient of the term) multiplied by zero or more variables (which are usually represented by letters). Each variable may have an exponent that is a non-negative integer. The exponent on a variable in a term is equal to the degree of that variable in that term. Since x = x1, the degree of a variable without a written exponent is one. A term with no variables is called a constant term, or just a constant. The degree of a constant term is 0. The coefficient of a term may be any number, including fractions, irrational numbers, negative numbers, and complex numbers.
For example,
is a term. The coefficient is –5, the variables are x and y, the degree of x is two, and the degree of y is one.
The degree of the entire term is the sum of the degrees of each variable in it. In the example above, the degree is 2 + 1 = 3.
A polynomial is a sum of terms. For example, the following is a polynomial:
It consists of three terms: the first is degree two, the second is degree one, and the third is degree zero. Here "− 5x" stands for "+ (−5)x", so the coefficient of the middle term is −5.
When a polynomial in one variable is arranged in the traditional order, the terms of higher degree come before the terms of lower degree. In the first term above, the coefficient is 3, the variable is x, and the exponent is 2. In the second term, the coefficient is –5. The third term is a constant. The degree of a non-zero polynomial is the largest degree of any one term. In the example, the polynomial has degree two.
[edit] Alternative forms
An expression that can be converted to polynomial form through a sequence of applications of the commutative, associative, and distributive laws is usually considered to be a polynomial. For instance,
is a polynomial because it can be worked out to x3 + 3x2 + 3x + 1. Similarly,
is considered a valid term in a polynomial, even though it involves a division, because it is equivalent to  and
and 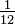 is just a constant. The coefficient of this term is therefore
is just a constant. The coefficient of this term is therefore 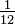 . For similar reasons, if complex coefficients are allowed, one may have a single term like (2 + 3i)x3; even though it looks like it should be worked out to two terms, the complex number 2+3i is in fact just a single coefficient in this case that happens to require a "+" to be written down.
. For similar reasons, if complex coefficients are allowed, one may have a single term like (2 + 3i)x3; even though it looks like it should be worked out to two terms, the complex number 2+3i is in fact just a single coefficient in this case that happens to require a "+" to be written down.
Division by an expression containing a variable is not generally allowed in polynomials.[1] For example,
is not a polynomial because it includes division by a variable. Similarly,
is not a polynomial, because it has a variable exponent.
Since subtraction can be treated as addition of the additive opposite, and since exponentiation to a constant positive whole number power can be treated as repeated multiplication, polynomials can be constructed from constants and variables with just the two operations addition and multiplication.
[edit] Polynomial functions
A polynomial function is a function defined by evaluating a polynomial. A function ƒ of one argument is called a polynomial function if it satisfies
for all arguments x, where n is a nonnegative integer and a0, a1,a2, ..., an are constant coefficients.
For example, the function ƒ, taking real numbers to real numbers, defined by
is a polynomial function of one argument. Polynomial functions of multiple arguments can also be defined, using polynomials in multiple variables, as in
Polynomial functions are an important class of smooth functions.
[edit] Polynomial equations
A polynomial equation is an equation in which a polynomial is set equal to another polynomial.
is a polynomial equation. In case of a polynomial equation the variable is considered an unknown, and one seeks to find the possible values for which both members of the equation evaluate to the same value (in general more than one solution may exist). A polynomial equation is to be contrasted with a polynomial identity like (x + y)(x – y) = x2–y2, where both members represent the same polynomial in different forms, and as a consequence any evaluation of both members will give a valid equality.
Graphs
A polynomial function in one real variable can be represented by a graph.
- The graph of the zero polynomial
-
- f(x) = 0
- is the x-axis.
- The graph of a degree 0 polynomial
-
- f(x) = a0 , where a0 ≠ 0,
- is a horizontal line with y-intercept a0
- The graph of a degree 1 polynomial (or linear function)
-
- f(x) = a0 + a1x , where a1 ≠ 0,
- is an oblique line with y-intercept a0 and slope a1.
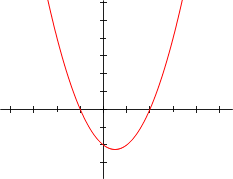
- The graph of a degree 2 polynomial
-
- f(x) = a0 + a1x + a2x2, where a2 ≠ 0
- is a parabola.
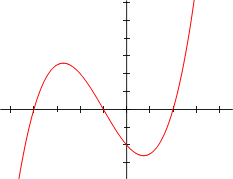
- The graph of any polynomial with degree 2 or greater
-
- f(x) = a0 + a1x + a2x2 + . . . + anxn , where an ≠ 0 and n ≥ 2
- is a continuous non-linear curve.
Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.
The illustrations below show graphs of polynomials.
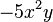

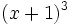
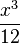
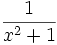


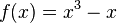

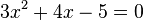



No comments:
Post a Comment