Solution of Triangle
From Wikipedia, the free encyclopedia
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ABC.
Types of triangles
Triangles can be classified according to the relative lengths of their sides:
- In an equilateral triangle, all sides are of equal length. An equilateral triangle is also an equiangular polygon, i.e. all its internal angles are equal—namely, 60°; it is a regular polygon.[1]
- In an isosceles triangle, two sides are of equal length (originally and conventionally limited to exactly two).[2] An isosceles triangle also has two equal angles: the angles opposite the two equal sides.
- In a scalene triangle, all sides have different lengths. The internal angles in a scalene triangle are all different.[3]
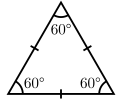 | 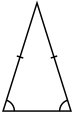 | 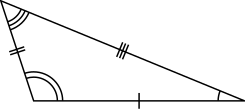 |
| Equilateral | Isosceles | Scalene |
Triangles can also be classified according to their internal angles, described below using degrees of arc:
- A right triangle (or right-angled triangle, formerly called a rectangled triangle) has one 90° internal angle (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side in the right triangle. The other two sides are the legs or catheti (singular: cathetus) of the triangle.
- An oblique triangle has no internal angle equal to 90°.
- An obtuse triangle is an oblique triangle with one internal angle larger than 90° (an obtuse angle).
- An acute triangle is an oblique triangle with internal angles all smaller than 90° (three acute angles). An equilateral triangle is an acute triangle, but not all acute triangles are equilateral triangles.
 | 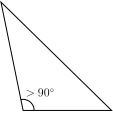 | 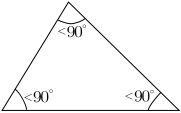 |
| Right | Obtuse | Acute |
 | ||
| Oblique | ||
Computing the area of a triangle
Calculating the area of a triangle is an elementary problem encountered often in many different situations. The best known and simplest formula is:
where S is area, b is the length of the base of the triangle, and h is the height or altitude of the triangle. The term 'base' denotes any side, and 'height' denotes the length of a perpendicular from the point opposite the side onto the side itself.
Although simple, this formula is only useful if the height can be readily found. For example, the surveyor of a triangular field measures the length of each side, and can find the area from his results without having to construct a 'height'. Various methods may be used in practice, depending on what is known about the triangle. The following is a selection of frequently used formulae for the area of a triangle.[4]
[edit] Using vectors
The area of a parallelogram can be calculated using vectors. Let vectors AB and AC point respectively from A to B and from A to C. The area of parallelogram ABDC is then  , which is the magnitude of the cross product of vectors AB and AC.
, which is the magnitude of the cross product of vectors AB and AC.  is equal to
is equal to  , where h represents the altitude h as a vector.
, where h represents the altitude h as a vector.
The area of triangle ABC is half of this, or  .
.
The area of triangle ABC can also be expressed in terms of dot products as follows:
[edit] Using trigonometry
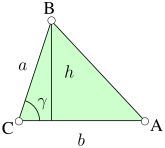
The height of a triangle can be found through an application of trigonometry. Using the labelling as in the image on the left, the altitude is h = a sin γ. Substituting this in the formula S = ½bh derived above, the area of the triangle can be expressed as:
Furthermore, since sin α = sin (π - α) = sin (β + γ), and similarly for the other two angles:
[edit] Using coordinates
If vertex A is located at the origin (0, 0) of a Cartesian coordinate system and the coordinates of the other two vertices are given by B = (xB, yB) and C = (xC, yC), then the area S can be computed as ½ times the absolute value of the determinant
For three general vertices, the equation is:
In three dimensions, the area of a general triangle {A = (xA, yA, zA), B = (xB, yB, zB) and C = (xC, yC, zC)} is the Pythagorean sum of the areas of the respective projections on the three principal planes (i.e. x = 0, y = 0 and z = 0):
Using Heron's formula
The shape of the triangle is determined by the lengths of the sides alone. Therefore the area S also can be derived from the lengths of the sides. By Heron's formula:
where s = ½ (a + b + c) is the semiperimeter, or half of the triangle's perimeter.
Three equivalent ways of writing Heron's formula are
Computing the sides and angles
In general, there are various accepted methods of calculating the length of a side or the size of an angle. Whilst certain methods may be suited to calculating values of a right-angled triangle, others may be required in more complex situations.
[edit] The sine and cosine rules
The law of sines, or sine rule[5], states that the ratio of the length of a side a to its corresponding angle A is equal to the ratio of the length of a side b to its corresponding angle B.
The law of cosines, or cosine rule, connects the length of an unknown side of a triangle to the length of the other sides and the angle opposite to the unknown side. As shown in the accompanying diagram, given two known lengths of a triangle a and b, and the angle between the two known sides γ (or the angle opposite to the unknown side c), to calculate the third side c, the following formula can be used:
[edit] Trigonometric ratios in right triangles

In right triangles, the trigonometric ratios of sine, cosine and tangent can be used to find unknown angles and the lengths of unknown sides. The sides of the triangle are known as follows:
- The hypotenuse is the side opposite the right angle, or defined as the longest side of a right-angled triangle, in this case h.
- The opposite side is the side opposite to the angle we are interested in, in this case a.
- The adjacent side is the side that is in contact with the angle we are interested in and the right angle, hence its name. In this case the adjacent side is b.
[edit] Sine, cosine and tangent
The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case
Note that this ratio does not depend on the particular right triangle chosen, as long as it contains the angle A, since all those triangles are similar.
The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. In our case
The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In our case
The acronym "SOHCAHTOA" is a useful mnemonic for these ratios.
[edit] Inverse functions
The inverse trigonometric functions can also be useful when trying to determine the remaining two angles of a right triangle when you already know the length of the sides of the triangle. Using the inverse sine or arcsine, we can use a simple ratio to calculate an angle from the ratio of two sides:
Often, the hypotenuse is unknown and would need to be calculated before using arcsin or arccos. Arctan comes in handy in this situation. You can compute the angle of the triangles without knowing the length of the hypotenuse.
For example, you can calculate the slope of a roof line if you know the rise and run of the roof. If the roof drops 8 feet (a negative rise of 8) as it runs out 20 feet (a positive run of 20), then your roof is angled θ degrees up from horizontal, where θ may be computed as follows:


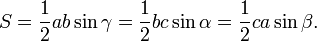

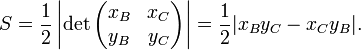


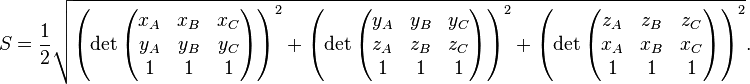




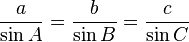


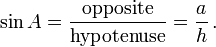
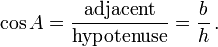
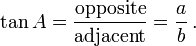

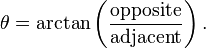
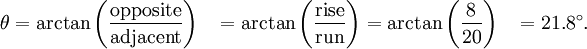








![\begin{align} \cos \alpha \,\cos \beta &= \frac{1}{2}[\cos(\alpha - \beta) + \cos (\alpha + \beta)]\\ \sin \alpha \,\sin \beta &= \frac{1}{2}[\cos(\alpha - \beta) - \cos (\alpha + \beta)]\\ \cos \alpha \,\sin \beta &= \frac{1}{2}[\sin(\alpha + \beta) - \sin (\alpha - \beta)]\\ \sin \alpha \,\cos \beta &= \frac{1}{2}[\sin(\alpha + \beta) + \sin (\alpha - \beta)] \end{align}](http://upload.wikimedia.org/math/f/7/2/f72c407d5a3a7a095152b883bfe2b65f.png)

 is correct, it means it may be either one, depending on the value of A/2.
is correct, it means it may be either one, depending on the value of A/2.
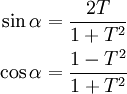
 .
.

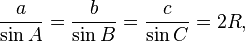
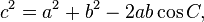

![\frac{a+b}{a-b}=\frac{\tan\left[\tfrac{1}{2}(A+B)\right]}{\tan\left[\tfrac{1}{2}(A-B)\right]}](http://upload.wikimedia.org/math/8/e/c/8ecc3d7514a107662d79d2b6e0678995.png)
